挑战程序设计竞赛（第2版）1.6.1 先从简单题开始 — 三角形

题目

有n根棍子，棍子i的长度为ai。想要从中选出3根棍子组成周长尽可能长的三角形。请输出最大的周长，若无法组成三角形则输出0。

限制条件

3 ≤ n ≤ 100
1 ≤ ai ≤ 10^6

输入

n = 5
a = {2, 3, 4, 5, 10}

输出

12（选择3、4、5时）

输入

n = 4
a = {4, 5, 10, 20}

输出

0（无论怎么选都无法组成三角形）

题目分析

选择3根棍子，它们能组成三角形的充要条件为最长棍子的长度 < 其余两根棍子的长度之和。
这里稍微解释一下，任意两边之和大于第三边、任意两边之差小于第三边、最长的边小于其余两边之和，这三句话是等价的，只要满足任意一个就都ok了。
书中给出了时间复杂度为O(n^3)的算法，三重循环，遍历每一种情况，找到最大的周长。
书中说还有复杂度为O(nlogn)的算法，留给读者思考。

O(nlogn)的算法

因为我们寻找的是最大周长，所以可以先将n条边a1到an从小到大排序，选择最大的那一条边an当作三角形中最长的边，然后判断a(n-2)+a(n-1)是否大于an，如果成立那么a(n-2)+a(n-1)+an就是答案。如果不成立，那么选择a(n-1)当作三角形中最长的边，然后判断a(n-3)+a(n-2)是否大于a(n-1)，同上，以此类推。
这样，排序的复杂度是 O(nlogn)，寻找答案的复杂度是O(n)，所以这个算法的复杂度是O(nlogn)

代码

上面分析中的边是a1到an，代码中的边是a[0]到a[n-1]

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int i, n, a[105], ans = 0;
    cin >> n;
    for (i = 0; i < n; i++)
        cin >> a[i];
    sort(a, a + n);
    for (i = n - 1; i >= 2; i--)
    {
        if (a[i] < a[i - 1] + a[i - 2])
        {
            ans = a[i] + a[i - 1] + a[i - 2];
            break;
        }
    }
    cout << ans << endl;
    return 0;
}

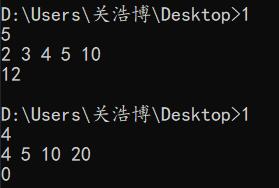
运行测试

如果代码写的不对，欢迎大家批评指正！