十大排序C语言实现

0 对比

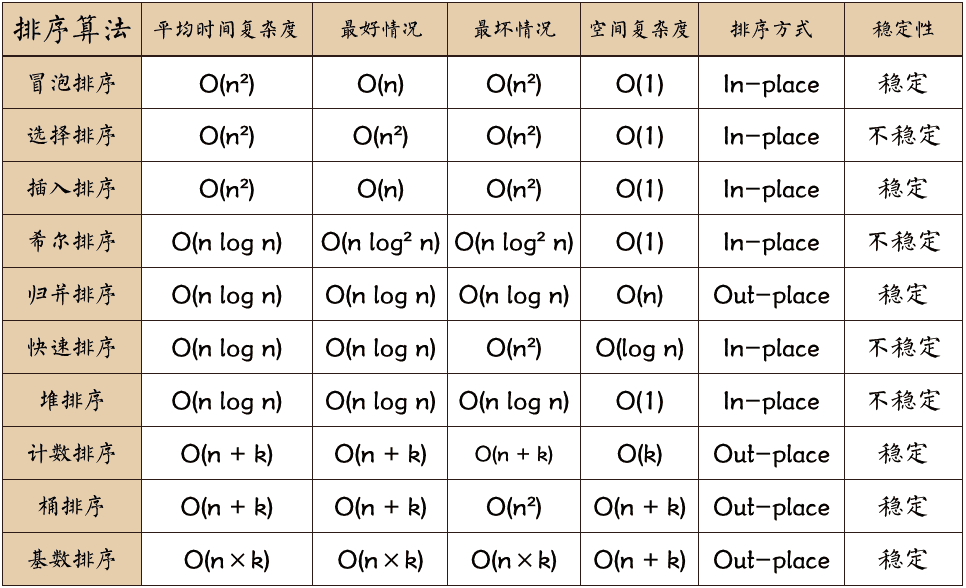
In-place：占用常数内存，不占用额外内存
Out-place：占用额外内存
稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

本文所有排序代码都是以从小到大排序来举例。

1 冒泡排序

原理：比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

第一轮冒泡后，数组的最后一个数字是最大的，第二轮确定出第二大的。每一轮冒泡结束，都会在数组的尾部确定下来一个数字，这个数字在以后的冒泡中是无需再进行访问的。

实现：一共需要进行len-1轮冒泡，所以外层循环次数是len-1；内层循环枚举未排好的数字，如果当前数字大于右边的数字，则进行交换。

时间复杂度O(n*n)

void bubble_sort(int arr[], int len)
{
    int temp;
    for (int i = 0; i < len - 1; i++)
    {
        for (int j = 0; j < len - i - 1; j++)
        {
            if (arr[j] > arr[j + 1])
                temp = arr[j], arr[j] = arr[j + 1], arr[j + 1] = temp;
        }
    }
}

上面的代码是从左到右冒泡，每次确定一个最大的。还可以从右到左冒泡，每次确定一个最小的，代码如下。

void bubble_sort(int arr[], int len)
{
    int temp;
    for (int i = 0; i < len - 1; i++)
    {
        for (int j = len - 1; j > i; j--)
        {
            if (arr[j] < arr[j - 1])
                temp = arr[j], arr[j] = arr[j - 1], arr[j - 1] = temp;
        }
    }
}

2 选择排序

原理：每次遍历一遍数组，寻找一个最小（或最大）的数字，然后将它和目标位置交换。

实现：一共需要遍历n-1次，所以外层循环次数为n-1；内层循环遍历没有排好的数字，找出最小（或最大）值；找到最值后将它和目标位置交换。

时间复杂度O(n*n)

void selection_sort(int arr[], int len)
{
    for (int i = 0; i < len - 1; i++)
    {
        int maxindex = 0, temp;
        for (int j = 0; j < len - i; j++)
        {
            if (arr[j] > arr[maxindex])
                maxindex = j;
        }
        temp = arr[maxindex], arr[maxindex] = arr[len - i - 1], arr[len - i - 1] = temp;
    }
}

上面的代码是每次寻找最大值，放在数组的尾部。还可以每次寻找最小值，放在数组的头部，代码如下。

void selection_sort(int arr[], int len)
{
    for (int i = 0; i < len - 1; i++)
    {
        int minindex = len - 1, temp;
        for (int j = len - 1; j >= i; j--)
        {
            if (arr[j] < arr[minindex])
                minindex = j;
        }
        temp = arr[minindex], arr[minindex] = arr[i], arr[i] = temp;
    }
}

3 插入排序

原理：从下标1开始遍历x，x左边是有序的。每次向有序数列中插入一个数字x，在x左边从右向左遍历，如果arr[j]大于x，将arr[j]向右移动一个位置，直到找出最左边的大于x的位置，将x放到这个位置即可。

时间复杂度O(n*n)

void insertion_sort(int arr[], int len)
{
    for (int i = 1; i < len; i++)
    {
        int j = i - 1, x = arr[i];
        while (j >= 0 && x < arr[j])
        {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = x;
    }
}

也可以从右向左枚举x，使得右边是有序的，代码如下。

void insertion_sort(int arr[], int len)
{
    for (int i = len - 1; i >= 0; i--)
    {
        int j = i + 1, x = arr[i];
        while (j < len && x > arr[j])
        {
            arr[j - 1] = arr[j];
            j++;
        }
        arr[j - 1] = x;
    }
}

4 希尔排序

待更新。

5 归并排序

原理：将数组分为左右两个小数组，对小数组进行归并排序，然后合并两个数组。
使用递归实现。递归的出口是数组元素等于1或2.

时间复杂度O(n*log(n))

void merge_sort(int arr[], int len)
{
    //递归出口
    if (len == 1)
        return;
    if (len == 2)
    {
        if (arr[0] > arr[1])
            arr[0] = arr[0] + arr[1], arr[1] = arr[0] - arr[1], arr[0] = arr[0] - arr[1];
        return;
    }
    //分成两个数组
    int *arr1 = (int *)malloc(sizeof(int) * len / 2);
    int *arr2 = (int *)malloc(sizeof(int) * (len - len / 2));
    for (int i = 0; i < len / 2; i++)
        arr1[i] = arr[i];
    for (int i = len / 2; i < len; i++)
        arr2[i - len / 2] = arr[i];
    //对两个数组分别进行归并排序
    merge_sort(arr1, len / 2);
    merge_sort(arr2, len - len / 2);
    //合并两个数组
    int i = 0, j = 0, index = 0;
    for (; i < len / 2 && j < len - len / 2; index++)
    {
        if (arr1[i] < arr2[j])
            arr[index] = arr1[i++];
        else
            arr[index] = arr2[j++];
    }
    //剩下的
    while (i < len / 2)
        arr[index++] = arr1[i++];
    while (j < len - len / 2)
        arr[index++] = arr2[j++];
}

6 快速排序

原理：找一个目标值x，一般是第一个或最后一个数。使用两个指针从两头到中间进行遍历，把小于x的和大于x的进行交换。当两个指针相遇的时候左边都小于x，右边都大于x。最后把x插入到中间（就是找个数交换一下位置），然后分别对两边进行快速排序。

时间复杂度`O(n*log(n))

void quick_sort(int arr[], int begin, int end)
{
    if (begin >= end)
        return;
    int target = arr[begin];
    int left = begin + 1, right = end, temp;
    while (left < right)
    {
        if (arr[left] <= target)
            left++;
        else if (arr[right] >= target)
            right--;
        else
            temp = arr[left], arr[left] = arr[right], arr[right] = temp;
    }
    if (arr[left] >= target)
        left--;
    temp = arr[left], arr[left] = arr[begin], arr[begin] = temp;
    quick_sort(arr, begin, left);
    quick_sort(arr, left + 1, end);
}

对快排进行改进，直接每次寻找中间那个数作为target，不必考虑target的位置是否发生变化，最后target会被移动到中间。
代码如下：

void quick_sort(int arr[], int begin, int end)
{
    if (begin >= end)
        return;
    int target = arr[(begin + end) / 2];
    int left = begin, right = end, temp;
    while (left < right)
    {
        while (arr[left] < target)
            left++;
        while (arr[right] > target)
            right--;
        if (left <= right)
        {
            temp = arr[left], arr[left] = arr[right], arr[right] = temp;
            left++, right--;
        }
    }
    quick_sort(arr, begin, right);
    quick_sort(arr, left, end);
}

7 堆排序

待更新。

8 计数排序

原理：开一个很大的计数数组，标记每个数字出现的次数。之后遍历计数数组即可。

void counting_sort(int arr[], int len)
{
    int maxv = arr[0], minv = arr[0];
    for (int i = 0; i < len; i++)
    {
        if (arr[i] > maxv)
            maxv = arr[i];
        if (arr[i] < minv)
            minv = arr[i];
    }
    int *vis = (int *)malloc(sizeof(int) * (maxv - minv + 1));
    memset(vis, 0, sizeof(int) * (maxv - minv + 1));
    for (int i = 0; i < len; i++)
        vis[arr[i] - minv]++;
    int index = 0;
    for (int i = minv; i <= maxv; i++)
    {
        while (vis[i - minv])
        {
            vis[i - minv]--;
            arr[index++] = i;
        }
    }
}

9 桶排序

待更新。

10 基数排序

待更新。